Kolmogorov microscales

Kolmogorov microscales are the smallest scales in turbulent flow. They are defined^[1] by

Kolmogorov length scale	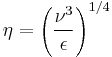$\eta = \left( \frac{\nu^3}{\epsilon} \right)^{1/4}$
Kolmogorov time scale	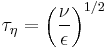$\tau_\eta = \left( \frac{\nu}{\epsilon} \right)^{1/2}$
Kolmogorov velocity scale	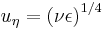$u_\eta = \left( \nu \epsilon \right)^{1/4}$

where $\epsilon$ is the average rate of energy dissipation per unit mass, and $\nu$ is the kinematic viscosity of the fluid.

In his 1941 theory, A. N. Kolmogorov introduced the idea that the smallest scales of turbulence are universal (similar for every turbulent flow) and that they depend only on $\epsilon$ and $\nu$ . The definitions of the Kolmogorov microscales can be obtained using this idea and dimensional analysis. 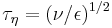Since the dimension of kinematic viscosity is length²/time, and the dimension of the energy dissipation rate per unit mass is length²/time³, the only combination that has the dimension of time is $\tau_\eta=(\nu / \epsilon)^{1/2}$ which is the Kolmorogov time scale. Similarly, the Kolmogorov length scale is the only combination of $\epsilon$ and $\nu$ that has dimension of length.

The Kolmogorov 1941 theory is a mean field theory since it assumes that the relevant dynamical parameter is the mean energy dissipation rate. In fluid turbulence, the energy dissipation rate fluctuates in space and time, so it is possible to think of the microscales as quantities that also vary in space and time. However, standard practice is to use mean field values since they represent the typical values of the smallest scales in a given flow.

References

^ Landahl, M.T. & E. Mollo-Christensen. Turbulence and Random Processes in Fluid Mechanics. Cambridge, 2ed, 1992.

Kolmogorov microscales

See also

References